数字图像处理练习题

1. 图像放大缩小

• 题目： 设一幅大小为M×N的灰度图像I中，现要变成（放大或缩小）为 P×Q的图像J，请写出J的生成算法。【参考函数：imresize】

• 解答：

  算法流程为：

  1. 通过原始图像大小和目标图像大小，确定横轴纵轴缩放因子\(t_1, t_2\)，并创建目标图像。
  2. 对目标图像的一个像素位置\((x',y')\)，根据缩放因子算出映射在原始图像的位置\((x,y)\)
  3. 对于整数值\((x,y)\)位置，直接将原始图像素值赋给目标图\((x',y')\)位置，对于非整数\((x,y)\)位置，使用插值法（双线性内插法）利用原始图\((x,y)\)相邻四个像素值计算目标像素点值赋给目标图\((x',y')\)位置。
  4. 重复2-3步骤直到目标图所有像素写完毕。

  算法具体运算细节即插值方法描述：设原始图像用\(f(x,y)\)表示，原图像大小为\(M×N\)，缩放后的图像为\(f(x',y')\)，其大小为\(P×Q\), 则在x方向缩放因子\(t_1=P/M\), y轴方向上的缩放因子为\(t_2=Q/N\)。则对于目标图像\(f(x',y')\)来说，对于每个像素点位置\((x',y')\),其映射再原图上的坐标位置\((x,y)\)有如下关系：\[x=x'/t_1 ,y=y'/t_2\] (1) 对于上式映射的\((x,y)\)都是整数的点，直接将原图对应位置像素值赋给目标图\((x',y' )\)位置。(2) 对于\((x,y)\)存在小数的情况，则需要使用插值(插值方法有很多，这里使用双线性内插法)法获得对应坐标值，这样对目标图每一个坐标都寻找到用原图像素映射的值，缩放结果图也便形成。

  双线性内插法介绍：需要找到原图中与\((x,y)\)位置最近的四个点设为\(Q_{11}(x_{1}, y_{1})\), \(Q_{12}(x_{1}, y_{2})\), \(Q_{21}(x_{2}, y_{1})\), \(Q_{22}(x_{2}, y_{2})\)。其位置关系如下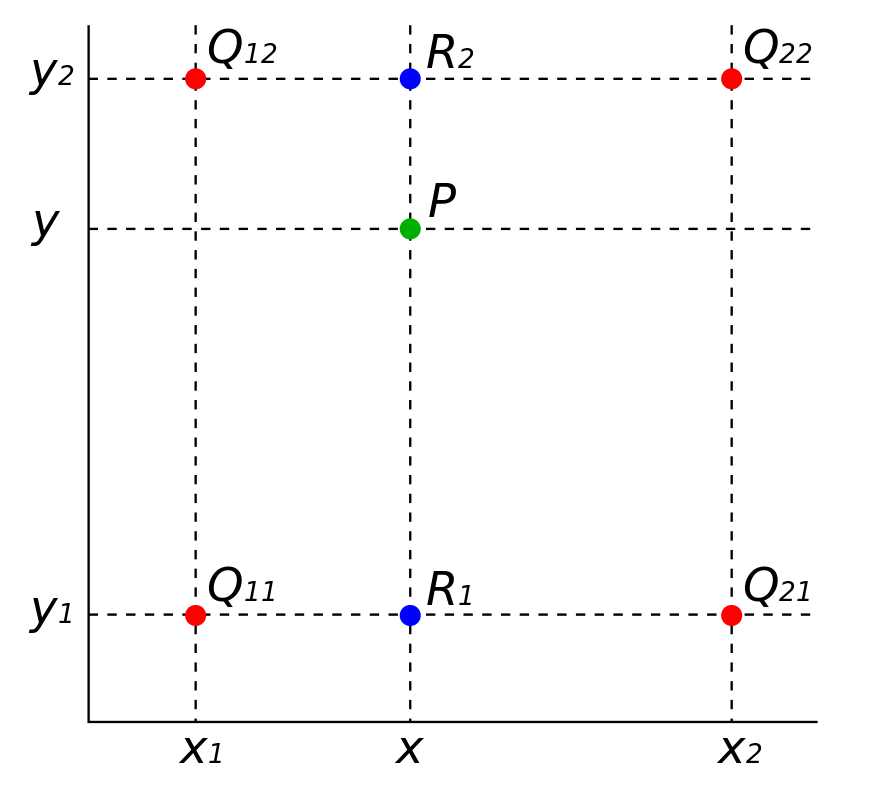： 如图所示，我们要求P点位置像素值，所以先用关于X的单线性插值去分别计算R1、R2的像素值： <img src="https://cdn.jsdelivr.net/gh/izhuhaoran/ImgsBed/CourseNoteImgs/202301241814131.png" width="50%/> 再使用关于y方向的单线性插值计算P点的像素值，得出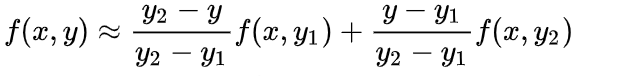： 在上面的等式中的字母y1、y2、y都是已知的，f(x,y1)与f(x,y2）即为上一个式子中求出的R1、R2像素值。

 

2. 中值滤波

• 题目1：请写出使用大小为3×3的模板对图像I进行中值滤波，生成图像J的方法。

• 解答：算法流程描述如下：

  1. 获得源图像的首地址及图像的宽和高
  2. 初始化目的图像，用以暂存结果图像，并初始化为0
  3. 初始模板中心在(2,2)位置，逐个扫描图像中的像素点，将其3*3邻域各元素的像素值从小到大进行排序，将求得到的中间值赋值给目标图像中与当前点对应的像素点。
  4. 循环步骤3,行列滑动模板位置，直到处理完源图像的全部像素点

注意：步骤3中的循环扫描不能从(1,1)位置开始，模板为3*3，初始状态中心应该在(2,2)位置

matlab代码如下：

clear;
A=imread('num22",'bmp);
subplot(1,2,1);
B=rgb2 gray(A);
subimage(B);
title('处理前的图);

C=B;
xsize=size(B);
for k=2:(xsize(1)-1)
    for j=2:(xsize(2)-1)
        t=B(k-1:k+1,j-1:j+1);
        C(k.j)=median(t(1:9));
    end
end

subplot(1,2,2);
subimage(C);
title('处理后的图);

 

• 题目2：简述中值滤波的特性和适用场合。

• 解答：中值滤波是一种非线性滤波，由于它在实际运算过程中并不需要图像的统计特性，所以比较方便。中值滤波首先是被应用在一维信号处理技术中，后来被二维图像信号处理技术所应用。在一定的条件下，可以克服线性滤波器所带来的图像细节模糊，而且对滤除脉冲干扰及图像扫描噪声最为有效。中值滤波的目的是保护图像边缘的同时去除噪声。

 

3. 傅里叶变换

• 题目1： 写出一维、二维离散傅立叶变换、反变换的计算公式。傅立叶系数的物理含义是什么？简述对一个二维图像进行快速傅里叶变换的方法。

• 解答：

  一维傅里叶变换(上)与反变换（下）：

  

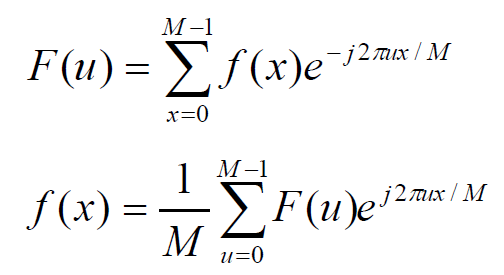
  二维傅里叶变换(上)与反变换（下）：

  

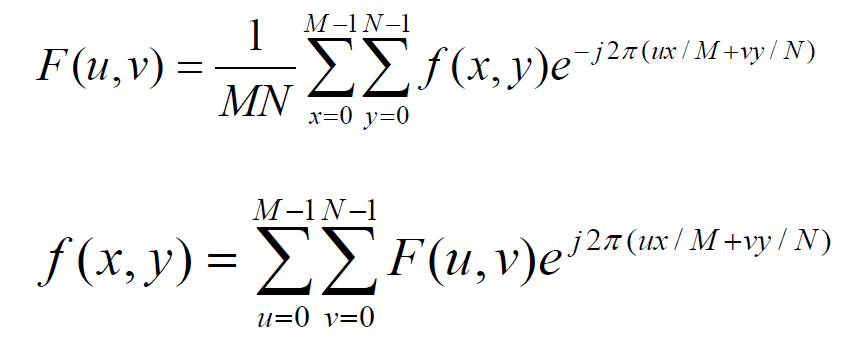
  傅立叶系数的物理含义：

  傅里叶变换可以看做“数学的棱镜”，将时域信号分解为若干不同频率的频域信号，而不同傅立叶系数则代表了分解的不同频率信号的振幅。

  二维图像进行快速傅里叶变换简述步骤：

  假设图像为一个M行N列的二维图像，用\(f(x,y)\)表示, FFT变换结果为\(F(u,v)\)简述对其二维FFT步骤为：

  1. 根据基2快速傅里叶变换的计算要求，需要图像的行数M、列数N均满足2的n次方，如果不满足，在计算FFT之前先要对图像补零以满足2的n次。
  2. 先按列变量y做一次长度为N的一维快速傅里叶变换FFT得到\(F(x,v)\): \[F(x,v)=\frac{1}{N} \sum_{y=0}^{N-1}{f(x,y)e^{-j2\pi vy/N}}, v=0,1,..,N-1 \]
  3. 再将第2步骤所得结果按x做一次长度为M的一维快速傅里叶变换得到最终结果\(F(u,v)\): \[F(u,v)=\frac{1}{M} \sum_{x=0}^{N-1}{F(x,v)e^{-j2\pi ux/M}}, u=0,1,..,N-1 \]

  上述流程中使用了一维FFT，原理主要是将长序列DFT分解为若干短序列DFT，利用旋转因子W的周期性，对称性，可约性减少计算量。 一维快速傅里叶(基2时分)原理具体介绍如下：

  1. 假设信号序列为\(x(n)\)，将其分解为偶数和奇数两个子序列即\(x(n)=x_1(n)+x_2(n)\), 两个子序列的长度都是N/2，\(x_1(n)\)是偶数序列，\(x_2(n)\)是奇数序列，则有：

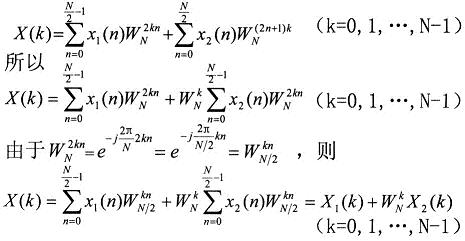
  2. 其中\(X_1(k)\)和\(X_2(k)\)分别为\(x_1(n)\)和\(x_2(n)\)的 N/2 点DFT。由于\(X_1(k)\)和\(X_2(k)\)均以 N／2为周期，且\(W_N^{k+N/2}=-W_N^k\)，所以\(X(k)\)又可表示为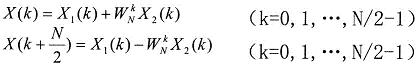： 即我们把一个N点的DFT拆成了两个N/2的DFT。

  3. 上述步骤2只是一次划分，经过若干次递归迭代二分划分，则原本的DFT（普通傅里叶）的\(O(n^2)\)时间复杂度 降为FFT（快速傅里叶）的\(O(n·log n)\)。

   

七、边缘检测

1、canny算子

• 题目：请写出Canny算子检测边缘的详细步骤。

• 解答：Canny边缘检测算法可以分为以下5个步骤

  1. 应用高斯滤波来平滑图像，目的是去除噪声。 总结一下这一步：高斯滤波其实就是将所指像素用周围的像素的某种均值代替(即卷积核)，卷积核尺寸越大，去噪能力越强，因此噪声越少，但图片越模糊，canny检测算法抗噪声能力越强，但模糊的副作用也会导致定位精度不高。
  2. 找寻图像的强度梯度。
  3. 根据梯度方向，对梯度强度幅值应用非最大抑制（non-maximum suppression），以消除边缘检测带来的杂散响应。
  4. 用双阈值算法检测检测来确定真实的和潜在的边缘，并通过抑制孤立的弱边缘最终形成结果边缘.
     • 选取系数TH和TL，比率为2:1或3:1。（一般取TH=0.3或0.2,TL=0.1）；
     • 将小于低阈值的点抛弃，赋0；将大于高阈值的点立即标记（这些点为确定边缘点），赋1或255；
     • 将小于高阈值，大于低阈值的点使用8连通区域确定（即：只有与TH像素连接时才会被接受，成为边缘点，赋 1或255）

 

八、形态运算

1、图像腐蚀

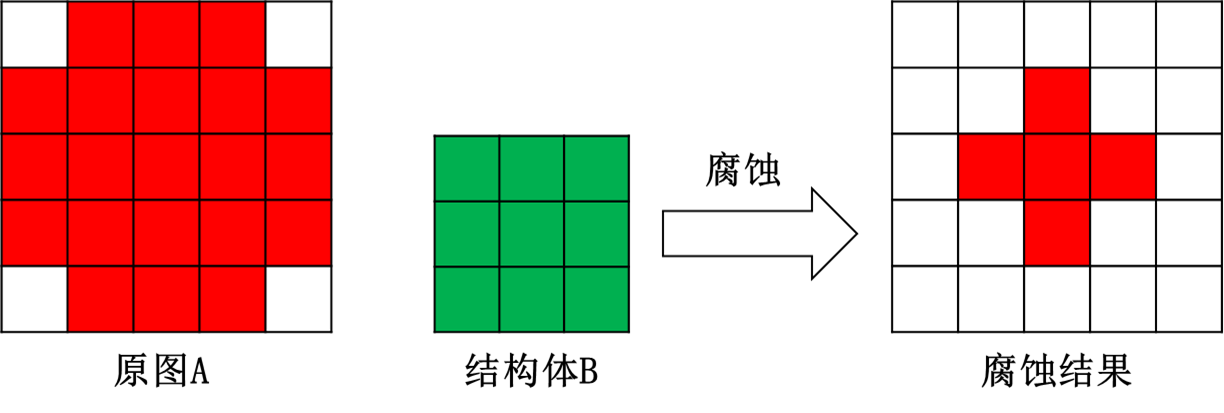
• 题目：设有一幅二值图像，采用 3×3的结构元（每个元素均为1）对其进行腐蚀操作，试写出得到结果图像的方法。

• 解答：腐蚀处理的结果是使原来的二值图像减小一圈, 原图A被结构B腐蚀的定义如下，z代表B的中心位置:

  \[A\bigodot B=\{z| (B)_z \subseteq A \}\] 可以理解为，移动结构B，如果结构B完全属于原图A的区域内，则保存该位置点，所有满足条件的点构成结构A被结构B腐蚀的结果。

  用结构体B对原图A进行腐蚀的整个过程如下： ⑴ 将3*3的结构元B在A中移动，即让B的中心循环扫描图像A的每一个像素。 ⑵ 用结构元素B的每个位置与其覆盖的二值图像同样位置做“与”操作 ⑶ 如果(2)结果中所有像素结果都为1，也即结构体B完全包含在A中，则此时目标图像对应B的中心位置像素为1，否则为0。

  示例结果如下, 有颜色代表像素为1，空白代表像素为0 ：

 

2、孔洞填充

• 题目：试写出孔洞填充的算法。对二值图像中所有被白色区域包围（封闭）的黑色像素即为孔洞。

• 解答：孔洞填充的公式为：

  \[X_k=(X_{k-1} \oplus B) \cap A^c \qquad k=1,2,3,...\]

  设原包含孔洞的图像为A，原图补集为\(A^c\)，用于填充膨胀的结构体为B，则孔洞填充算法流程：

  1. 将原图像A每个像素取反，获得补集原图像的补集记作\(A^c\)，用来限制膨胀结果在孔洞内，防止膨胀超出孔洞区域范围；
  2. 在原图孔洞中选择一个初始点，使用结构体B膨胀该点；
  3. 将膨胀后的结果与原图补集\(A^c\)相交，得到该轮次的结果\(X_k\)。
  4. 在原图孔洞中移动到下一个点，重复2~4步，直到第K步和第K+1步结果相同，填充完毕。

  上述算法步骤中使用了膨胀操作，下面简述膨胀操作过程： 膨胀处理的结果是使原来的二值图像扩大一圈, 原图A被结构B膨胀的定义如下，z代表B的中心位置:

  \[A\bigoplus B=\{z| (\hat{B})_z \bigcap A \neq \emptyset\}\] 上式中\((\hat{B})_z\)是结构体关于中心圆点反转的结构，膨胀可以理解为，移动结构B的反转结构\((\hat{B})_z\)，如果与原图A存在重叠区域，也即交集不为空，则此时结构体中心位置对应在目标图结果中处像素为1，反之没有交集则为0。

 

3、粘连区域断开

• 题目：设有两个白色区域，被一条细小的白线所连接，试设计一种算法，消除两个区域之间的细线，使两个区域分开。

• 解答：使用开运算即可，开运算等于对原图先腐蚀后膨胀，可以用来消除小物体、在纤细点处分离物体、消除物体周围的毛刺等。设原图为A，结构体为B开运算的公式为：

  \[A \bigcirc B=(A\odot B) \oplus B\]

  分割两个细小白线连接的白色区域的步骤如下：

  1. 设置开运算结构B为N*N, N的大小根据细线的宽度而更改，要比细线宽度大。
  2. 先对原图A使用结构体B进行腐蚀运算。
  3. 对2的结果再次使用结构体B进行膨胀运算。

  注意，上述开运算步骤中使用了腐蚀和膨胀运算，这两种算法见前两题图像腐蚀和孔洞填充中介绍，这里不再赘述。

 

4、计算凸壳

• 题目：计算包围给定点集的最小凸多边形。

• 解答：采用安德鲁算法计算最小凸包，流程简述如下： （1）将给定的点集合按照x坐标升序排列。x相同的话，按照y坐标升序排列 （2）创建凸包的上部U点序列：默认将x最小的两个点加入上凸包U，再将排序后的点按照x坐标从小到大的顺序依次加入凸包U，并检查U是否仍然为凸包。如果新加入的点使得U不再是凸多边形，那么就逆序依次删除已经插入U的点，直到U为凸多边形。 （3）创建凸包的下部L点序列：默认将x最大的两个点加入下凸包L, 再将排序后的点按照x坐标从大到小的顺序加入凸包L，并检查L是否仍然为凸包。如果新加入的点使得L不再是凸多边形，那么就逆序删除已经插入L的点，直到L为凸多边形。 （4）连接凸包的上部和下部： 最终外接凸多边形点集为凸包上部的点序列+凸包下部逆置后的点序列(下部形成是按照x从大到小，要逆序形成从小到大的序列)，每两个点之间连线，最后一个点和第一个点连线即是最终外接凸多边形。

  检查是否为凸包的方法如下： 设将要加入点\(P_2\)，凸包集中上一轮加入的节点为\(P_1\), 上上一轮加入的节点为\(P_0\) , 则形成两个向量： \(\vec{a}=P_0 \rightarrow P_1\)和 \(\vec{b}=P_0 \rightarrow P_2\)。如果\(\vec{a} \times \vec{b} < 0\), 则说明第二个向量\(\vec{b}\)位于第一个向量\(\vec{a}\)的逆时针处, 此时新加入节点\(P_2\)会使结果不再是凸边形，需要逆序删除已经插入的点，直到加入\(P_2\)后，保持凸包。

  上述判断方法示意图如下, 此时加入P2会使第二个向量\(\vec{b}\)位于第一个向量\(\vec{a}\)的逆时针处，凸包被破坏，需要逆序删除P1点。